key:知识运算,重复博弈
\def\sube{\subseteq} $\def\sube{\subseteq}$
$\color{red}{一门政管开的通选课}$
主要知识点
均衡的求法
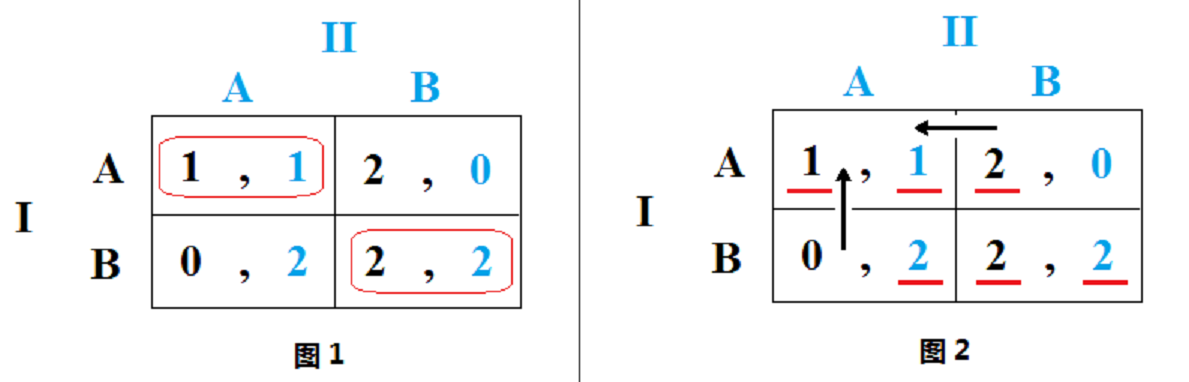
- 划线法求纯策略均衡
- 重复剔除严格劣策略
- 利用“充要条件”求混合策略均衡
- 行为策略均衡的求法
- 逆向归纳法求子博弈精炼均衡
- 贝叶斯均衡的求法
- 利用“四个要求”求精炼贝叶斯均衡
- 序贯均衡的求法
- 精炼贝叶斯均衡的再精炼
策略的概念
- 纯策略
- 混合策略
- 行为策略
- 混合策略和行为策略的互相转化
- 相关策略
理性的概念
- 认知理性
- 工具理性
特殊的专题
序贯均衡,纳什谈判- 重复博弈(无限次重复,有限次重复)
拍卖(静态,动态,收益等价定理)- 知识的运算
完全信息静态博弈
纯策略与混合策略
双人零和博弈
- 零和博弈属于严格竞争博弈
- 对于双人有限策略零和博弈,我们可以从双变量矩阵中省略列参与 者的收益,故这种博弈又称矩阵博弈。
- 行参与者是最大最小策略,列参与者是最小最大策略。
纳什均衡
- 严格纳什均衡和弱纳什均衡的差别是,能不能用 $\ge $ 替换 $>$。
混合策略纳什均衡的充分必要条件是:对于任何一个参与者,凡是以正德概率被选择德从混策略应带来相等的期望收益,且不低于以零概率被选择的纯策略带来的期望收益。
- 方法:构造一个一般化的混合策略组合,然后检查是否满足。对所有子集组合重复分析。
*有限博弈,纳什均衡存在。几乎所有的有限博弈都具有有限的奇数个均衡。(?)
占优策略
- 特定策略优于或至少不劣于其它任何策略。
- 占优策略均衡是指每个参与者都存在占优策略,这些占优策略构成的组合。
可理性化
如果无论参与者对于世界状态持有的信念如何,参与者的某一选择都不是最优反应,则为永非最优策略。如果存在一个(混合)策略,使得无论世界状态如何,某一特定始终低于该(混合)策略带来的收益,则该特定策略称为严格劣策略。
占优定理:如果选择集和世界状态集都是非空有限集,那么严格劣策略等于永非最优策略。
如果参与者的某一策略关于对手策略选择的任何信念都不是最优反应,那么称该策略是永非最优反应。理性人不应当采取永非最优反应。
一个策略是可理性化。是说所有参与者都是理性的是共同知识。

重复剔除严格劣策略
- 双人博弈中,参与者的策略是永非最优反应当且仅当它是严格劣的。
- 从理性共识出发可以重复剔除严格劣策略,最后剩下的如果只剩下一个,这个策略组合是重复剔除的占优均衡
- 在双人博弈中,可理性化的策略 等价于 不能被重复剔除 严格劣策略过程所剔除的策略。
- 对于超过两人的博弈,可理性化的策略一定是不能被重复 剔除严格劣策略过程所剔除的策略,但反之则未必。
- 理性共识,零阶理性公式:每个人都是理性的,不知道对方是不是理性。……
纳什均衡与重复剔除的占优均衡的关系
- 纳什均衡不会被重复剔除严格劣策略过程所剔除。
- 如果重复剔除严格劣策略过程最终只剩下唯一的策略组合,那么这一策略组合为该博弈唯一的纳什均衡。
- 重复剔除弱劣策略过程有可能剔除弱纳什均衡,但不会剔除严格纳什均衡。
多重纳什均衡的比较
参与者集合的任何子集称为联盟,如果存在联盟使得成员协调行动一起偏离均衡能够提高每个成员的收益叫做这个联盟能瓦解纳什均衡。如果不存在则为强均衡。
完美均衡:允许颤抖,如果存在严格混合策略序列,使得即使这一步错了,剩下的策略还是最优策略。
- 每个有限博弈至少有一个(颤抖手)完美均衡。进一步,在(颤抖手)完美均衡中,没有人使用 (严格以及弱)劣策略。
- 在二人有限策略博弈中,不含弱劣策略的纳什均衡都是(颤抖手)完美均衡。
- 风险占优
- 假设对手采用各个纳什均衡对应策略的概率相同,计算并比较 自己采用纳什均衡对应策略能获得的期望收益,我们说,能带来更 高期望收益的策略所对应的纳什均衡“风险占优”于另一个纳什均衡
- 偏离损失乘积比较法,即分别计算各个参与者独自偏离当前均衡而遭受的损失,计算偏离损失的乘积(简称“纳什积”),该乘积更大的均衡“风险占优”。
相关策略、相关均衡和相关理性化
相关策略:
- $G={N,(S_i),(u_i)}$,参与者集合,纯策略组合,相关策略 $\alpha$ 就是定义在纯策略集的笛卡尔积上的一个概率分布。
相关均衡
- 玩家可以选择遵循相关策略 $\alpha$ ,也可以不选择。
- 当违背约定的期望收益不如遵守约定时,所有玩家就都会遵守约定了,这就是相关均衡。
相关均衡的计算
- 线性规划,增加一些限制,即背离了均衡效用小于零。
相关理性化
- 在允许各个对手采取相关策略的情况下,可理性化称为相关理性化。
完全信息动态博弈
行为策略均衡
混合策略均衡的多重性
- 策略性表述:针对不同信息集给结论
- 多代理人表述:假装有多个人在选
行为策略
(0.5[a1]+0.5[b1], [y1])- 混合策略
0.5[a1y1]+0.5[b1z1],0.5[a1y1]+0.5[b1y1] - 行为上等价:当且仅当两个混合策略具有相同的行为表示时,称这两 个混合策略是行为上等价的。
- 收益等价: 如果无论其他参与者采取怎样的混合策略,博弈的每个参与者的期望收益都不依赖于参与者 i 采取混合策略 A 或混合策略 B,就称参与者 i 的混合策略 A 与 B 是收益等价的。
- 在一个具有完美回忆的博弈中,两个行为上等价的混合策略 也一定是收益等价的。
- 行为策略均衡:为了避免多重均衡和无意义均衡这两个问题,对于扩展型博弈,我们一般考虑行为策略均衡,它被定义为其多代理人表示的任一均衡 $σ$ ,并要求 $σ$ 的混合表示同时也是其策略型正规表示的一个均衡。
- 求法:首先将它转化为策略型表述,然后求出一个混合策略纳什均衡,再以行为策略表示之。第一步求出的行为策略组合就是一个行为 策略均衡。
威胁的可信性与子博弈精炼均衡
一种威胁所规定的行动在事前看来是最优的,但事后看并不 是参与者的最优选择,这种威胁就是不可信的,含有这种威 胁的策略就不是一个合理的策略。
子博弈要求
- 始于博弈树中一个单节信息集,但不包括博弈的根节点
- 包含该决策节点之后所有的决策节点和终节点;
- 没有分割任何信息集。
子博弈精炼均衡:每一个子博弈都是纳什均衡,排除了不可置信的威胁。
- 一个解指一条均衡路径。
- 一次偏离性质与逆向归纳法
- 无限连续多阶段可观察行动博弈
- 某一策略组合构成子博弈精炼纳什均衡的 充分必要条件是它满足如下“一次偏离性质”:
- 不可能在某个子博弈的时候进行改变从而提高自己的收益。
- 因此可以倒着来树形动态规划求子博弈精炼纳什均衡。
谈判专题
- 序贯谈判
- 纳什谈判
- 有一个谈判破裂点 $(d_1,d_2)$
- 纳什谈判解唯一,$\arg \max (x_1-d_1)(x_2-d_2)$
正向归纳法
- 参与者在形成自己的信念时,应该考虑本可能发生却没有发生的事情,因此,参与者除了从后面逆向推理外,还应该从博弈树的初始节点向前推理。
重复博弈
- 1、如果对于每一个参与者可以找到一个均衡解,超过它的最小最大值,那么重复博弈博弈就可以收敛到这个附近。
- 2、如果阶段博弈 G 有唯一的纳什均衡,则对任意有限的 T , 重复博弈 G(T) 有唯一的子博弈精炼解,即 G 的纳什均衡结果在每一阶段重复出现。
- 3、如果有唯一的逆向归纳解,对于任意有限的T,有唯一的子博弈精炼解,每一阶段都是G的逆向归纳解。
- 重复博弈,足够耐心,相对确定的环境可以让欺骗行为得到察觉,有奖有罚且受骗人有积极性乘法,乘法的规格必须既充分又适度。
*博弈学习理论与均衡的稳定性
不完全信息静态博弈
博弈的表述
参与者集合;状态(state)集合;每个参与者的行动(action);每个参与者的信号(signal)集合,以及状态和信号联系起来的信号函数;信念(belief):对于可能接收到的每个信号,与该信号相一致的各个状态出现的概率,参与者要有一个具体的信念;收益函数
海萨尼转化指的是引入一个新的参与者(自然),从而将不完全信息变为关于自然行动的不完美信息。
知识的运算
- “事件”是 Y 的子集。所以可以说:事件 A 在状态 w 下成立。
- 参与者 $i$ 知道事件 $A$ 成立,记作 $K_iA$,这是一个事件,得到的也是一个状态的集合。
- 定理1:所以一是对于每个事件 $A \sube Y$ 和每个参与者 $i \in N$ , $K_iA \sube A$ 。
- 定理2:$A\sube B\Rightarrow K_iA\sube K_iB$。
- 一个知识其实是可以当作一个分割。
博弈的分析
- 事前占优与事中占有
贝叶斯均衡
- 对于可能接收到的每一个信号,他都要选择一个行动
- 可以将原来不完全信息静态博弈的纳什均衡定义为多代理人表述的完全信息静态博弈的纳什均衡
- 对于可能接收到的每一个信号,他都要选择一个行动
拍卖机制设计与显示原理
直接机制:是指每个参与者的行动空间就是其类型空间的静态贝叶斯博弈,即让参与者报告其类型。
间接机制:需要从参与者所选择的行动去推断其类型。
显示原理:任何贝叶斯博弈的任何纳什均衡,都可以重新表示为一个激励相容的直接机制。
所谓重新表示,是指对参与者的任何可能的类型组合, 新的均衡下参与者的行动和收益与旧的均衡下完全相同。
所谓激励相容,是指每个参与者讲真话构成一个贝叶斯纳什均衡。
tips:机制设计在小铁的算法博弈论里说得挺好的,VCG拍卖等等。可惜我没有两门课都没有好好学,小铁的课直接退了。
不完全信息动态博弈
- 子博弈概念的扩展
- 使用“后续博弈(continuation game)”来代替“子博弈”的概念。
- 两类信息集:
- 正的概率到达
- 根据均衡策略肯定不会到达(均衡路径之外的信息集)
均衡:纳什均衡、子博弈精炼均衡以及精炼贝叶斯均衡
- 精炼贝叶斯均衡
- 在每一个信息集之中,应该行动的参与者必须对博弈进行到该信息集之中的哪一个节点有一个推断。belief
- 必须满足序贯理性,现在的行为以及随后的策略在根据给定该参与者在此信息集中的 推断,以及其他参与者随后的策略(随后可能的策略),必须是最优反应。
- 在处于均衡路径之上的信息集之中,推断由贝叶斯法则及参与者的均衡策略给出。
- 对处于均衡路径之外的信息集,推断由贝叶斯法则以及可能情况下的参与者的均衡策略给定。
序贯均衡- 借鉴完美均衡中的颤抖思想,使得每个参与者在每个信息集的每个行动都以正概率被选择,进而依据贝叶斯法则生成推断(取极限)组合,并要求各参与者的行为策略在该推断组合下满足序贯理性的要求。该行为策略组合和推断组合称为一个序贯均衡。
精炼贝叶斯均衡的再精炼信号博弈与信息传递
- 私人信息的拥有者可以进行 信号发送,不掌握私人信息的一方可以 信号甄别。
- 分离均衡;混同均衡;半分离均衡(杂合均衡)
- 信息传递博弈(information-transmission games) 或称廉价交谈(cheap talk)
- 胡言乱语均衡(babbling equilibrium)
非理性与声誉
- KMRW(1982)的模型表明,如果参与者对其他参与者的收益函数和策略空间的信息不完全,即使博弈重复的次数是有限的,人们也有积极性建立一个合作的声誉 (reputation),合作会出现。
- 单方面不完全信息可能会导致合作的出现。
- 一些没用的碎碎念
- 博弈论的基本假定。参与者是理性的,博弈的结构是参与者的共同知识,每个参与者都可以看到博弈树。所有参与者具有完美回忆。
- 如果这是一个Nash Equilibrium,每个人都没有偏离均衡的动机。partial是零或者考虑边界情况。
- 对于可能纯策略和混合策略,分开讨论,谁纯策略,谁混合策略,首先剔除严格劣策略。
- 对于两人的动态博弈,行为策略表示类似$(([R] , 1/3[R]+2/3[F]) , 2/3[M]+1/3[P])$ ,这个表示在其中一种信息集的情况下选R,一种情况混合策略,对于参与者二则信息集不会分割。三人也类似。首先可以考虑混合策略表示,然后把混合策略用行为策略表示。
- 同样可以先求出策略性表述,然后转化成行为策略。行为策略也可以看成是不同信息集下逐步的选择。
- 如果用逆向归纳法求(纯策略)子博弈精炼纳什均衡的话,行为表述不能省略,子博弈要求把所有的博弈内容都输出来,也就是把子树的结果也应该输出。
- 多阶段博弈如果一个阶段有唯一的纳什均衡那就是它了(?)
- 寡头垄断企业效用最大化的话,分阶段考虑,可以用逆向归纳法。(其实最后一次作业最后一题也是逆向归纳法应该)首先考虑最后一个阶段单点信息集的最大效用。
- 重复博弈有一个贴现因子 $\delta$,可以考虑一直不合作的效用,在第 $k$ 个阶段开始合作的效用。【冷酷策略】是说如果对方某次选择了不合作,则永远不合作。对于无限次重复博弈其实是能得到一个不等式
- 考虑子博弈精炼纳什均衡,一定先考虑逆向归纳法?(对于完全信息)。注意求导是根据原式求的。
- 对于不完全信息博弈可以搞知识的运算,你处于某个信息集中需要满足这个信息集的所有单点都是你可能处于的位置。这是知识算子 $K$ 的定义。
- 对于进入市场和不进入市场的问题, 一旦不进入市场后期也不会进入市场了。
- 如果某个人的效用函数可以不是随机变量构成的话,其实是可以求导进行效用最大化的。如果是随机变量的话,就是让期望效用最大化。逐步消除变量,让变量越少越好。
- 关于不完全信息动态,策略型表示纯策略划线可以搞。
- 精炼贝叶斯均衡是关于信念的。
- 策略… 与 信念 … 可以作为精炼贝叶斯均衡。
- 具体计算方法是
- 考虑信念的范围,根据信念分类讨论。
- 根据策略分类讨论,比如分离均衡与混同均衡。
- 精炼贝叶斯均的再均衡与精炼贝叶斯均衡有一点差别,差别是:
- 精炼贝叶斯均衡排除了参与者 $i$ 选择的策略包含始于信息集的严格列策略的可能性,要令参与者 $j$ 相信参与者 $i$ 选择这样的策略就是不合理的。
- 纳什均衡:没有一个参与者选择严格劣策略
- 子博弈精炼纳什均衡:任何一个子博弈参与者也不会采取严格劣策略。
- 推广到后续博弈的情况:任何一个后续博弈中一个参与者不会采取严格劣策略。
- 均衡劣信号就是你最好也选不上这个。直观标准就是均衡劣信号不会被选。
- 精炼贝叶斯均衡要求你的信念一定要是合理的。
