最大熵强化学习——从概率图模型到SAC

CS285 Lec14: Control as Inference Problem - 知乎 (zhihu.com)

这个讲得是真的好

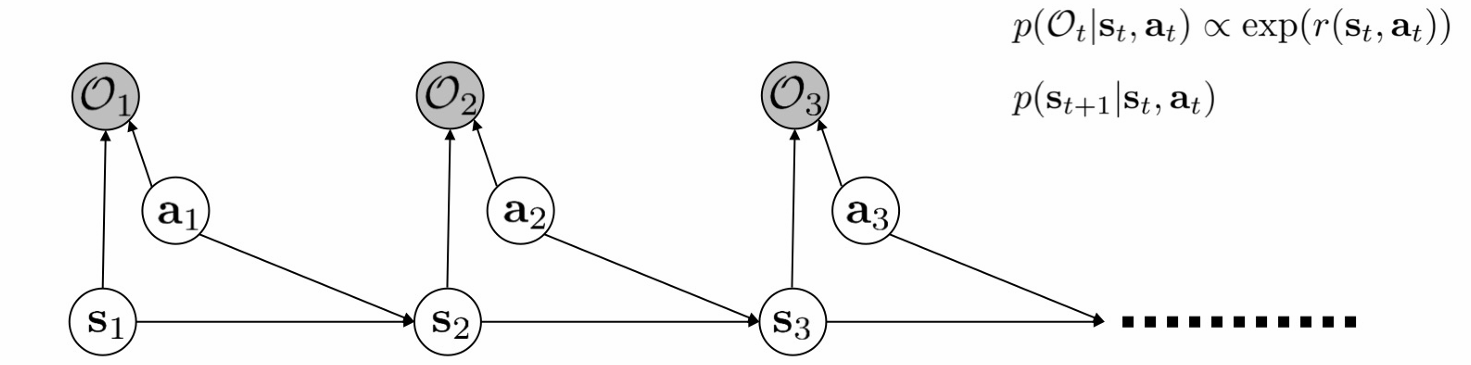
我们最初有的设定是

$$p(O_t\mid s_t,a_t)\propto \exp (r(s_t,a_t))$$

对于给定的一张概率图

$$\begin{align*} \beta_t(s_t,a_t)&=p(O_{t:T}\mid s_t,a_t)\\ &=\int p(O_{t:T},s_{t+1}\mid s_t,a_t) \mathrm d s_{t+1}\\ &=\int p(O_{t+1:T}\mid s_{t+1})p(s_{t+1}\mid s_t,a_t)p(O_t\mid s_t,a_t) \mathrm d s_{t+1} \end{align*}$$ $$\beta_t(s_{t+1})=p(O_{t+1:T}\mid s_{t+1})=\int p(O_{t+1:T}\mid {s_{t+1},a_{t+1}})p(a_{t+1}\mid s_{t+1})\mathrm d a_{t+1}$$ $$\beta_{t}(s_t,a_t)=p(O_t\mid s_t,a_t)\mathbb E_{s_{t+1}\sim p(s_{t+1}\mid s_t,a_t)}[\beta_{t+1}(s_{t+1})]\\ \beta_{t}(s_t)=\mathbb E_{a_t \sim p(a_t\mid s_t)}[\beta_t(s_t,a_t)]$$

let $V_t(s_t)=\log \beta_t(s_t)$, $Q_t(s_t,a_t)=\log \beta_t(s_t,a_t)$

if We take $p(a_t\mid s_t)$ as uniform,

$$V_t(s_t) = \log \int \exp(Q_t(s_t,a_t))\mathrm d a_t\\ Q_t(s_t,a_t)=r(s_t,a_t)+\log \mathbb E[\exp V_{t+1}(s_{t+1})]$$

注意这里如果直接做的话，Q关于V是要log sum exp的，后面我们会看到能把这个去掉。

Then we consider if $p(a_t\mid s_t)$ as a prior distribution which is not uniform.

$$V_t(s_t)=\log \int \exp(Q_t(s_t,a_t)+\log p(a_t\mid s_t)) \mathrm d a_t\\ Q_t(s_t,a_t)=r(s_t,a_t)+\log \mathbb E_{s_{t+1}}[\exp V_{t+1}(s_{t+1})]$$

so let

$$\tilde Q(s_t,a_t)=r(s_t,a_t)+\log p(s_t\mid a_t) + \log \mathbb E[\exp V(s_{t+1})]$$

Then

$$V(s_t)=\log \int \exp ({\tilde Q(s_t,a_t)})$$

so, the policy $\pi(a_t\mid s_t)$ which is

$$\begin{align*} p(a_t\mid s_t,O_{1:T})&=\pi(a_t\mid s_t)\\ &=\frac{p(a_t,s_t\mid O_{t:T})}{p(s_t\mid O_{t:T})}\\ &=\frac{p(O_{t:T}\mid a_t,s_t)p(s_t,a_t)/p(O_{t:T})}{p(O_{t:T}\mid s_t)p(s_t)/p(O_{t:T})}\\&=\frac{p(O_{t:T}\mid a_t,s_t)p(s_t,a_t)}{p(O_{t:T}\mid s_t)p(s_t)}\\ &=\frac{\beta_t(s_t,a_t)}{\beta_t(s_t)}p(a_t\mid s_t)\\ &= \frac{\beta_t(s_t,a_t)}{\beta_t(s_t)} \end{align*}$$

so we have

$$\pi(a_t\mid s_t)=\exp(Q_t(s_t,a_t)-V_t(s_t))=\exp A_t(s_t,a_t)$$

and temperature are allow to add.

Then we consider the optimism problem, for that

$$Q_t(s_t,a_t)=r(s_t,a_t)=\log E(\exp(V_{t+1}(s_{t+1})))$$

我们再回过头来回顾一下这些变量都代表什么意思：

$p(O_{t:T}\mid s_t,a_t)$：现在处于状态 $s_t$，选了方法 $a_t$，接下来能获得的得分的期望

$p(at\mid s_t,O{1:T})$：为了获得最大的得分，我在当前状态的期望是什么，也就是当前的policy

$p(st\mid O{1:{t-1}})$

$p(s{t+1}\mid s_t,a_t,O{1:T})$ 是如果能获得最大的分数，那么转移的概率是什么

$p(s_{t+1}\mid s_t,a_t)$ 是转移的概率，和上面一个不一样。

$$\begin{align*} p(\tau\mid O_{1:T})\propto&\ p(\tau,O_{1:T})\\ =&p(s_1)\prod _{t=1}^T p(O_{T}\mid s_t,a_t) p(s_{t+1}\mid s_t,a_t) \\ =&p(s_1)\prod _{t=1}^T \exp (r(s_t,a_t)) p(s_{t+1}\mid s_t,a_t) \\ =&\left[p(s_1)\prod_{t=1}^Tp(s_{t+1}\mid s_t,a_t)\right] \exp ({\sum_{i=1}^T r(s_t,a_t)}) \end{align*}$$

下面简记 $p(\tau) = p(\tau \mid O_{1:T})$

在这里，如果我们先假设

$$p(s_{t+1}\mid s_t,a_t,O_{1:T})=p(s_{t+1}\mid s_t,a_t)$$

，然后做如下推导

在给定最优变量 $O_{1:T}=1$ 的时候，整个概率图的轨迹分布可以表示为 $p(\tau)$

而给定策略 $\pi(a_t\mid s_t)$ 的时候，整条轨迹的分布表示为

$$\hat p(\tau)=p(s_1 \mid O_{1:T})\prod p(s_{t+1}\mid s_t,a_t,O_{1:T}) \pi(a_t\mid s_t) \\ \approx p(s_1)\prod p(s_{t+1}\mid s_t,a_t) \pi(a_t\mid s_t)$$

最小化两者的KL散度，也就是最大化负的散度

$$\begin{align*} -D_{KL}(\hat p(\tau)||p(\tau))=&\mathbb E_{\tau \in \hat p(\tau)} [ \log (p(s_1))+\sum_{t=1}^T(\log p(s_{t+1}\mid s_t,a_t)+r(s_t,a_t))\\ &-\log (p(s_1))-\sum_{t=1}^T(\log p(s_{t+1}\mid s_t,a_t)+\log \pi(s_t,a_t)) ]\\ =&\mathbb E_{\tau \in \hat p(\tau)}\left[\sum_{t=1}^T (r(s_t,a_t)-\log \pi(a_t\mid s_t)\right]\\ =&\sum_{t=1}^T \mathbb E_{(s_t,a_t) \sim \hat p(s_t,a_t)} [r(s_t,a_t)]+\mathbb E_{s_t \sim \hat p(s_t)} [\mathcal H(\pi(a_t\mid s_t))] \end{align*}$$

也就是按当前策略的方法去采样能获得的reward的情况。

如果去掉 $p(s{t+1}\mid s_t,a_t,O{1:T})=p(s_{t+1}\mid s_t,a_t)$，这个假设，那么应该有

$$\begin{align*} \hat p(\tau)=&p(s_1\mid O_{1:T}) \prod _{t=1}^T p(s_{t+1}\mid s_t,a_t,O_{1:T})p(a_t\mid s_t,O_{1:T})\\ \end{align*}$$

而

$$p(\tau)=\left[p(s_1)\prod_{t=1}^Tp(s_{t+1}\mid s_t,a_t)\right] \exp ({\sum_{i=1}^T r(s_t,a_t)})$$

这里的 p(tau) 意味着在后验分布的情况下的，

这两项之间如果还是求 KL 散度

$$\log p(s_1)-\log p(s_1\mid O_{1:T})+\sum_{t=1}^T\log p(s_{t+1}\mid s_t,a_t)\\-\sum_{t=1}^T \log p(s_{t+1}\mid s_t,a_t,O_{1:T}) + \sum_{t=1}^T (r(s_t,a_t)-\log \pi(a_t\mid s_t ))\\$$

据说是不太好优化的，我没具体搞懂

我们考虑变分推断，用一个简单的变分函数去近似后验分布

$$p(\tau)=\left[p(s_1)\prod _{t=1}^T p(s_{t+1}\mid s_t,a_t)\right]\exp (\sum_{t=1}^T{r(s_t,a_t)})$$

这里用一个函数 $q$

$$q(\tau)=q(s_1) \prod_{t=1}^T q(s_{t+1}\mid s_t,a_t) q(a_t\mid s_t)$$

如果我们假设 $x=O{1:T}, z=(s{1:T},a_{1:T})$，那么可以理解成我们想要的分布是 $p(z\mid x)$，我们想用分布 $q(z)$ 来逼近它。

$$\begin{align*} \log p(x) =&\log \int_{z} p(x,z)\\ =&\log \int_z p(x,z)\frac{q(z)}{q(z)}\\ =&\log \mathbb E_{q} \left[\frac{p(x,z)}{q(z)}\right]\\ \ge& E_{z\sim q(z)}[\log p(x,z)-\log q(z)] \end{align*}$$ $$\log p(\tau) \ge \mathbb E_{(s_{1:T},a_{1:T})\sim q}$$

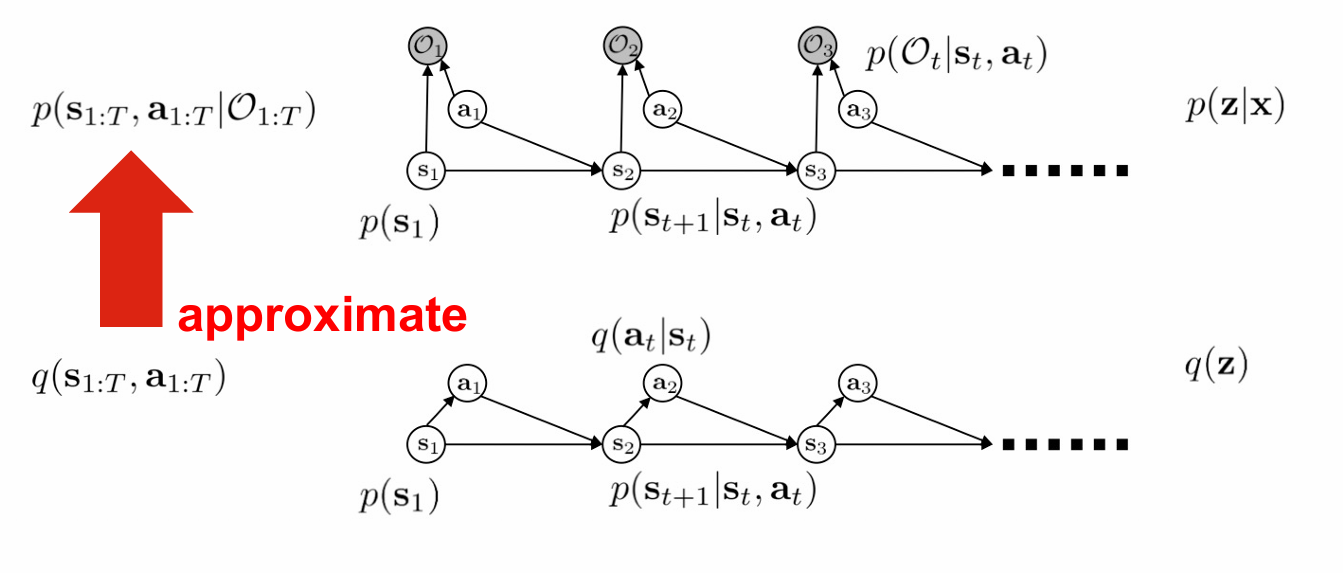
我们在这里给 $q$ 设置一个约束条件，使得 $q(s1)=p(s_1),q(s{t+1}\mid st,a_t)=p(s{t+1}\mid s_t,a_t)$ 成立，那么就能有

$$q(\tau)=p(s_1) \prod_{t=1}^T p(s_{t+1}\mid s_t,a_t) q(a_t\mid s_t)$$

于是

$$\log p(O_{1:T})\ge \mathbb E_{(s_t,a_t) \sim q(s_t,a_t)}\left[\sum_{t=1}^T (r(s_t,a_t)-\log q(a_t\mid s_t)\right]\\$$

在上文中我们记

$$L=\mathbb E_q[\log p(x,z)]+\mathcal H(z)$$

这里做一个补充，为什么我们需要 $\log p(x)$，考虑一个KL散度

$$\begin{align} K L[q(Z) \| p(Z | X)] &=\int_{Z} q(Z) \log \frac{q(Z)}{p(Z | X)} \tag{6}\\ &=-\int_{Z} q(Z) \log \frac{p(Z | X)}{q(Z)} \tag{7}\\ &=-\left(\int_{Z} q(Z) \log \frac{p(X, Z)}{q(Z)}-\int_{Z} q(Z) \log p(X)\right) \tag{8}\\ &=-\int_{Z} q(Z) \log \frac{p(X, Z)}{q(Z)}+\log p(X) \int_{Z} q(Z) \tag{9}\\ &=-L+\log p(X) \tag{10} \end{align}$$

上文中我们有

$$L=\log p(X)-K L[q(Z) \| p(Z | X)]$$

就是说如果估计分布和真实后验分布完美接近，那么这个 $L$ 就等于 $\log p(x)$。

我们型要让KL等于零，那么这里的log是多少？

所以我要优化这个KL尽可能地小，在 $\log p(x)$ 不变的情况下，我就去优化这个 $L$ 尽可能大。也就是这里的 $L$ 就变成了目标函数。天然地多出来一个 $\mathcal H(z)$

接下来我们呢继续推导 $q(a_T\mid s_T)$ 长什么样子

$$q(a_T\mid s_T)=\arg \max \mathbb E_{s_T\sim q(s_T),a_T\sim q(a_T\mid s_T)}\left[r(s_T,a_T)-\log q(a_T\mid s_T)\right]$$

可以解出来

$$q(a_T\mid s_T)\propto\ \exp(r(s_T,a_T))$$

也就是说，对于最后一个步骤

$$q(a_T\mid S_T)=\frac{\exp r(s_T,a_T)}{\int \exp (r(s_T,a))\mathrm da}=\exp(Q(s_T,a_T)-V(s_T))$$

这里设

$$V(S_T)=\log \int \exp(Q(s_T,a_T))\mathrm d a_T$$

同理得到对于中间的步骤

$$q(a_t\mid s_t)=\exp(Q(s_t,a_t)-V(s_t))$$

注意这里我们是从零开始的，也就是我们是有了 $q$ 的正比这个性质，从而定义了 $Q$，

$$Q(s_t,a_t)=r(s_t,a_t)+E[V_{t+1}(s_{t+1})]$$

这里没有logsumexp。

在这个基础上，我们试着得出 soft Q-learning

首先先看Q-learning with soft optimality，应该是这样的

$$\phi\leftarrow \phi+\alpha \nabla _{\phi}Q_\phi(s,a)(r(s,a)+\gamma V(s')-Q_\phi(s,a))$$

这里target value

$$V(s')=\text{soft}\max _{a'} Q_\phi(s',a')=\log \int \exp(Q_\phi(s',a'))da'$$

最后有

$$\pi(a\mid s)=\exp (Q_\phi(s,a)-V(s))=\exp (A(s,a))$$

我们考虑 soft Q learning的推导

Reinforcement Learning with Deep Energy-Based Policies

如果我们引入熵的话，我们想要有

$$\pi_{MaxEnt}^*=\arg \max_\pi \sum_{t=0} \mathbb E_{\rho_\pi}[\gamma^t(r_t+\alpha \mathcal H(\pi(\cdot \mid s_t)))]$$

在给定一个 $\pi$ 之后定义

$$Q_{soft}^\pi(s,a)\triangleq r(s_0,a_0)\mid_{s_0=s,a_0=a} + \mathbb E_{\tau \sim \pi}[\sum_{t=1}^\infty \gamma^t(r_t+\alpha \mathcal H(\pi(\cdot\mid s_t)))]\mid _{s_0=s,a_0=a}$$

那么最大熵策略的目标函数是

$$J(\pi)=\sum_t \mathbb E_{(s_t,a_t)\sim \rho_\pi}[Q_{soft}^\pi(s_t,a_t)+\alpha \mathcal H(\pi(\cdot \mid s_t))]$$

再来一个定义是

$$V_{soft}^\pi(s)\triangleq\alpha \log \int_A \exp(\frac{1}{\alpha}Q_{soft}^\pi{(s,a)})da\\ =\alpha \log \mathbb E_{q_a} \exp(\frac{1}{\alpha}Q_{soft}^\pi{(s,a)}-\log {q_a(a)})da$$

能够证明

$$Q_{soft}^\pi(s,a)=r(s,a)+\gamma \mathbb E_{s'}[V^\pi_{soft}(s')]$$

在这个基础上可以导出一个最优的policy

$$\tilde \pi(a\mid s)=\exp (\frac{1}{\alpha}({Q_{soft}^\pi(s,a)-V_{soft}^\pi(s))})$$

注意，这一项就是等号，不是一个正比号。

然后一个性质就是可以证明

$$Q_{soft}^\tilde \pi(s,\cdot )\ge Q_{soft}^\pi(s,\cdot )$$

暂且略去这个证明。

总之我们也有了单调递增性。

entropy-regularized policy gradient can be viewed as performing soft Q-learning on the maximum-entropy.

漫谈Entropy, Energy and Learning. - 知乎 (zhihu.com)

这里另一种方法是是基于能量的模型 EBM

$$\max_p \mathbb E_{x\sim p}[\phi(x)]+\alpha \mathcal H(p)$$

它的最优分布是玻尔兹曼分布

$$p^*(x)\propto\ e^{-\phi(x)/\alpha}$$

这里的 $\alpha$ 是一个温度的系数。

$$\mathbb E_{x\sim p}[\frac{\phi(x)}{\alpha}-\log p(x)]=-KL(p||p_\phi)$$

这里 $p_\phi(x)=\frac{e^{\phi(x)/\alpha}}{Z}=\frac{e^{-\mathcal E(x)}}{Z}$，其中 $\mathcal E(x)=-\phi(x)/\alpha$。

能量越低越容易保持在这样一个状态，能量越高越容易一晃而过。

从这个角度我们来看策略优化，在某个状态下去找

$$\text{soft} \max_a \mathbb E_{a\sim \pi(\cdot \mid s)}[Q(s,a)] + \alpha \mathcal H(\pi(\cdot \mid s))$$

就有

$$\pi^*(a\mid s)\propto \exp(Q(s,a)/\alpha)$$

从上文我们定义了soft的V和Q，我们有

$$V^\pi_{soft}(s_t)=\mathbb E_{a\sim \pi}[Q^\pi_{soft}(s_t,a_t)]+\alpha \mathcal H(\pi(\cdot \mid s_t)) \\Q_{soft}^\pi(s,a)=r(s,a)+\gamma \mathbb E_{s'}[V^\pi_{soft}(s')]$$

接着我们来说一下soft Q-learning，首先是去学习（更新）Qsoft

$$J_Q(\theta)=\mathbb E_{(s_t,a_t)}[\frac{1}{2}(r(s,a)+\gamma \mathbb E_{s'}[V^{\bar \theta}_{soft}(s')-Q^\theta_{soft}(s_t,a_t))^2]$$

因为希望通过当前的policy对Q更新， $V$ 要做一步重要性采样来算出来，前文提到的

$$V_{soft}^\theta(s_t)=\alpha \log \mathbb E_{\pi} \frac{ \exp(\frac{1}{\alpha}Q_{soft}^{\theta}{(s_t,a')}) }{\pi(a')}$$

但是 $\pi$ 还是不能直接通过贪心来求。

所以在 soft Q-learning 里面，通过最小化当前policy和基于价值函数构造出来的soft max分布的形式，用 SVGD 通过KL散度优化策略。（对于连续空间）

soft Actor-Critic 希望直接去优化策略

前文提到

$$\pi_{new}=\arg \min_{\pi'} D_{KL}(\pi'||\exp(Q^{\pi}old)/Z)$$

策略迭代能保证迭代之后的价值不小于迭代之前的价值。

所以这个方法的算法的细节包括如下两种

首先通过bellman方程迭代更新Q和V，使用两个Q网络，$\bar \psi=\tau \psi +(1-\tau)\bar \psi$。

还有一个策略函数的学习目标，通过正比于 $Q+\mathcal H$ 的方法，这是我们之前用概率图方法推导出来的。

$$J_\pi(\phi)=\mathbb E_{s_t\sim D,\epsilon _t\sim N}[\log \pi_\phi(f_\phi(\epsilon_t;s_t)\mid s_t)-Q_\theta(s_t,f_\phi(\epsilon_t;s_t))]$$

所以迭代更新。

实验：

认为它非常diverse，确实是鼓励了探索。

softQ作为预训练，对于不同的环境，也更好。

SAC认为策略用随机策略比固定策略更好，虽然一开始比较慢，但是最终会好。但是估值的时候相比于随机策略，用固定策略的更好。

---

我们来回顾一下这个 entropy 到底是哪里出现的。

最开始的目标函数中出现是因为我们用了变分不等式。

然后是值迭代的时候，$V$ 用 $\log \int \exp$ 来估计，这个 $\int$ 是平均意义上的，对于特定的策略的话就需要一个熵。