Inverse Reinforcement Learning

CS 285: Lecture 20, Inverse Reinforcement Learning, Part 1 (youtube.com)

CampusAI

lec-20.pdf (berkeley.edu)

The imitation learning perspective

Standard imitation learning:

• copy the actions performed by the expert
• no reasoning about outcomes of actions

Human imitation learning:

• copy the intent of the expert
• might take very different actions!

---

Inverse reinforcement learning

• Infer reward functions from demonstrations

• 给定了 $s\in S,a \in A,p(s’\mid s,a)$以及一些从 $\pi^*(\tau)$ 中采样的轨迹

• 求 $r_{\psi}(s,a)$ (reward parameters)
• 然后用它来求 $\pi^*(a\mid s)$

feature matching IRL

如果我们用linear的方法来建模reward function。

$$r_\psi(s,a)=\sum_i \psi_i f_i(s,a)=\psi^T f(s,a)$$

如果这些feature $f$ 是重要的：

我们想要 $\pi^{r\psi}$ 作为一个关于 $r\psi$ 的最优的policy，也就是希望

$$E_{\pi^{r_\psi}}[f(s,a)]=E_{\pi^*}[f(s,a)]$$

这里的

$$E_{\pi^*}[f(s,a)]=\sum_{(s,a)} f(s,a) \times \rho(s,a)$$

这里 $\rho(s,a)$ 表示在数据集中 $(s,a)$ 这样的pair出现了多少次。

而左边的部分，如果环境未知可以用sample的方法来作同样的事情（expensive but useful），如果环境不大而且已知可以用动态规划来学。

为了找到最佳的参数，借鉴SVM中的 maximum margin principle。

$$\max_{\psi,m} m;s.t. \psi^T E_{\pi^*}[f(s,a)] \ge \max_{\pi \in \Pi} \psi^T E_\pi[f(s,a)]+m$$

一个很启发式的方法，找到那个让expert非常厉害的 $\psi$。

$$\begin{equation} max_{\psi} \frac{1}{2} \Vert \psi \Vert^2 \space \space \space s.t. \psi^T E_{\pi^*} [f(s, a)] \geq max_{\pi \in \Pi} \psi^T E_{\pi} [f(s, a)] + D ( \pi, \pi^\star ) \end{equation}$$

Issues：

• Maximizing the margin is a bit arbitrary
• What if the “expert” demonstrations are suboptimal? We could add slack variables as in a SVM setup.
• It might be ok for this linear case but become very messy for ANN reward approximation.

optimal control as a model of human behavior

回到这张图

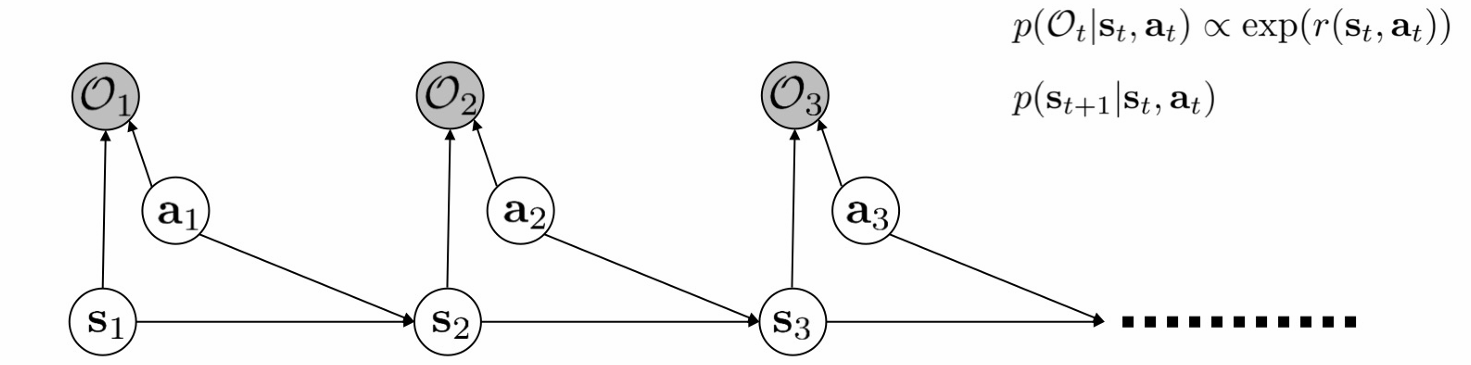
现在我们要inference the reward function.

这里 $\psi$ 是reward的一个参数。

$$p(O_t\mid s_t,a_t,\psi)=\exp(r_\psi(s_t,a_t))$$ $$p(\tau \mid O_{1:T}) \propto \exp(\sum_t r_\psi{(s_t,a_t)})$$

那么最大似然估计的方法，我们从 $\pi^*$ 中sample 一些 $\tau_i$

$$\max_\psi \frac{1}{N} \sum_{i=1}^N \log p(\tau_i\mid O_{1:T},\psi)=\max_\psi \frac{1}{N}\sum_{i=1}^N r_\psi(i)-\log Z$$

所以IRL partition function就是

$$\max_\psi \frac{1}{N}\sum_{i=1}^N r_\psi(i)-\log Z$$

这里的

$$Z=\int p(\tau)\exp(r_\psi(\tau)) d\tau$$

代入展开我们有

$$\begin{equation} \nabla_\psi \mathcal{L} = \frac{1}{N} \sum_i \nabla_\psi r_\psi (\tau_i) - \frac{1}{Z} \int p(\tau) exp(r_\psi(\tau)) \nabla_\psi r_\psi(\tau) d \tau \end{equation}$$

这里第二项就是 $\tau$ 发生的概率，也就写成

$$\begin{equation} \label{grad} \nabla_\psi \mathcal{L} = E_{\tau \sim \pi^\star (\tau)} \left[ \nabla_\psi r_\psi (\tau_i) \right] - E_{\tau \sim p(\tau \mid O_{1:T}, \psi)} \left[ \nabla_\psi r_\psi(\tau) \right] \end{equation}$$

展开

$$\begin{equation} E_{\tau \sim p(\tau \mid O_{1:T}, \psi)} \left[ \nabla_\psi r_\psi(\tau) \right] = \sum_t E_{(s_t, a_t) \sim p(s_t, a_t \mid O_{1:T}, \psi)} \left[ \nabla_\psi r_\psi(s_t, a_t) \right] \end{equation}$$

利用

$$p(s_t, a_t \mid O_{1:T}, \psi) = p(a_t \mid O_{1:T}, \psi) p(s_t \mid O_{1:T}, \psi)$$

得到

$$p(a_t \mid O_{1:T}, \psi) p(s_t \mid O_{1:T}, \psi) \propto \beta(s_t, a_t) \alpha(s_t)$$

那么如果定义

$$\mu_t(s_t, a_t) \propto \beta(s_t, a_t) \alpha(s_t)$$

就有

$$\begin{equation} E_{\tau \sim p(\tau \mid O_{1:T}, \psi)} \left[ \nabla_\psi r_\psi(\tau) \right] = \sum_t \int \int \mu_t(s_t, a_t) \nabla_\psi r_\psi(\tau) ds_t da_t = \sum_t \vec{\mu_t}^T \cdot \nabla_\psi \vec{r}_\psi \end{equation}$$

这样我们就得出了 MaxEnt IRL Algorithm

• AAAI08-227.pdf

关于为什么叫MaxEnt，据说是，在 $r\psi (s_t, a_t) = \psi^T f(s_t, a_t)$ 的时候他优化了 $max\psi \mathcal{H} \left( \pi^{r\psi} \right)
\space \space s.t.
E{\pi^{r\psi}}[f] = E{\pi^\star} [f]$

推导 【逆强化学习-2】最大熵学习（Maximum Entropy Learning）_最大熵逆向强化学习代码-CSDN博客 比较好，从最大熵的目标函数除法，利用拉格朗日乘子法重新得到了那个优化公式。

To apply this in practical problem settings, we need to handle…

1. Large and continuous state and action spaces
2. States obtained via sampling only
3. Unknown dynamics

注意我们的公式其实就是：

$$\begin{equation} \nabla_\psi \mathcal{L} \simeq \frac{1}{N} \sum_i \nabla_\psi r_\psi (\tau_i) - \frac{1}{M} \sum_j \nabla_\psi r_\psi (\tau_j) \end{equation}$$

第一项是expert的policy，第二项是目前的policy。

一个直观的想法是学习 $p(at \mid s_t, O{1:T}, \psi)$，不过这会比较慢。

一个想法是用一个分布 $\pi\theta(a_t\mid s_t)$ 去近似 $p(a_t \mid s_t, O{1:T}, \psi)$。那么从 $\pi_\theta$ 中取就需要一个重要性采样。

$$\begin{equation} \nabla_\psi \mathcal{L} \simeq \frac{1}{N} \sum_i \nabla_\psi r_\psi (\tau_i) - \frac{1}{\sum_j w_j} \sum_j w_j \nabla_\psi r_\psi (\tau_j) \end{equation}$$

这里 $wj = \frac{p(\tau) exp ( r\psi (\tauj) ) }{\pi\theta(\tauj)}$,展开的话就是 $w_j = \frac{exp \left( \sum_t r\psi (st, a_t)\right)}{\prod_t \pi\theta (a_t \mid s_t)}$。

所以假设我们已经有 $\pi\theta,\pi^*$ 之后，可以用 $\psi \leftarrow \psi + \alpha \nabla \psi L(\psi)$ 来更新 reward function。

在此之外，固定当前的reward function，对policy也可以更新

$$\nabla_\theta L(\theta)=\frac{1}{M} \sum_{j=1}^M \nabla_\theta \log \pi_\theta(\tau_j) r_\psi(\tau_j)$$

持续迭代更新reward function和policy。

其中Rewad Function往能使专家行为产生高价值同时使当前Policy行为产生低价值的方向跑，然后Policy往能在当前Reward下产生高价值的行为方向跑，从而又体现出了对抗的思想!

Inverse RL as a GAN

• Finn, Christiano et al. “A Connection Between Generative Adversarial Networks, Inverse Reinforcement Learning, and Energy-Based Models.”

假设读者已经对GAN有所了解，GAN的优化目标是

$$\psi=\arg \max_\psi \frac{1}{N}\sum_{x\sim p^*} \log D_\psi(x)+\frac{1}{M}\sum _{x \sim p_\theta}\log (1-D\psi (x))$$

而

$$\theta \leftarrow \arg \max_\theta E_{x\sim p_\theta}\log D_\psi(x)$$

注意到如果

$$D^*(x)=\frac{p^*(x)}{p_\theta(x)+p^*(x)}$$

那么这个判别器是最优的。

对于InverseRL我们知道 $\pi\theta(\tau) \propto p(\tau)\exp (r\psi(\tau))$

这里的

$$\begin{align*} D_\psi(\tau)=&\frac{p(\tau)\frac{1}{Z}\exp (r(\tau))}{p_\theta(\tau)+p(\tau)\frac{1}{Z}\exp (r(\tau))}\\ =&\frac{\frac{1}{Z}\exp (r(\tau))}{\prod_t \pi_\theta(a_t\mid s_t)+\frac{1}{Z}\exp (r(\tau))}\\ \end{align*}$$

这样的话就可以用GAN的思路来看待offline RL。

Can we just use a regular discriminator?